What is Binary?
How Do Computers Make Mistakes When Interpret Binary?
- Overflow Error
- Point-Float Error
How Do Computers Use Binary to Run?

What is Binary?

Binary is another method of keeping track of numbers using our modern symbols. Most people count using the decimal system, or Base 10. However, computers count using binary, also known as Base 2. I will be referring to decimal and binary as Base 10 and Base 2 respectively to make explantions clearer

Base 10 uses 10 symbols to represent numbers (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) while binary uses 2 symbols to represent numbers (0, 1). Some people forget to include 0 in this list but 0 represents the very important concept of a lack of a number.

Base 10 and Base 2 are very similar in the ways they work. For example, in Base 10 (standard counting) when we count to 9 and want to add 1 we add another digit to the number, the number then becomes 10. The same concept is applied to Base 2, but Base 2 only has two symbols so it occurs much more frequently. For example, we have the number 1 and want to add 1 in Base 2. Since there are no more symbols to show that 1 has increased. So we add another digit. and 1 becomes 10.

The same concept applies to further digits, when we add 10 and 4 in standard counting, it becomes 14. Base 2 is the same, when we add 10 and 1 we end up 11. If we add 1 to this number we follow the first concept we talked about. Then the number becomes 100.

How to Convert Binary to Decimal?

Converting between the two numbers is actually incredibly easy. It’s easier to convert from binary to decimal so we’ll explain this first. In order to convert from binary to decimal, just multiply each digit by 2^n^, with n being equal to the digits from the right starting from 0. For example, abcd is 4 digits, so we would multiply d by 2^0^, c by 2^1^, b by 2^2^, and a by 2^3^.

How to Convert Decimal to Binary?

In order to convert decimal to binary we follow a pattern. First we perform log~2~() on our number. This allows us to know the number of digits when rounded up. Then we will perform the modulo action on our number, with the output being equal to the digit. Then we subtract 2^n^, with n being the digit from the right starting at 0 if it outputs 1 and nothing if we output 0.

How to Do Binary Addition?

Binary addition is just like decimal division. You simply line the digits up and add them together, carrying over a number when it goes over the symbol limit, in this case 1. For example, 101 + 11, first add the first digit for both (1+1). This is greater than 1 so we carry over a 1 the second digit place and leave the remainder. Then the second digit will be 0 + 1 + 1, with the second one being our carry over. This means we have another carry over and we carry a 1 to the third digits. This gives us 1 + 1. When all of this is done it should result in 1000

How to Do Binary Subtraction?

See How to do Binary Addition? Apply this theory to subtraction

How to Do Binary Multiplication?

Binary multiplication is in some ways simpler than decimal multiplication. You can multiply a binary number by a power of 2 extremely easily, by simply shifting the entire number n digits, with n being equal to log~2~() of the number you are multiplying by. Otherwise, we have to do the same strategy as decimal multiplication and do repeated addition while multiplying numbers.

How Do Computers Make Mistakes When Interpret Binary?

Computers are not like people and therefore interpret these numbers differently than we do, this leads to errors that a computer might have that a human would not. We go over the errors computers may make when reading a binary number here.

Overflow Error

Overflow error is the concept of a number growing so large that it resets or becomes negative. This is due to the nature of the way we store binary numbers in computers. In order to store negative values in computers we make the first digit determine positive or negativity. When the first digit is 0 the number is positive, and vice versa. However, when a number grows large enough, when the math is done it increases the final digit with the carry over. Causing the number to be flipped and be negative. The number will become more and more negative the more that is added due to it hitting the integer limit.

Point-Float Error

Binary is only so precise, having more symbols makes decimal have more accurate fractional representation, with binary this is simply not possible. For example, computers cannot perfectly represent 0.3. This is due to the fact that we can’t represent 3 in one spot with binary, the closest that we can do is 0.01001100110011…, this means that when we add 0.1 and 0.2, which should equal 0.3, we get a this number which is not perfectly accurate. This is generally fixed by cutting the number off after a certain amount of digits so that the excess is not seen. Also known as truncating the number.

How Do Computers Use Binary to Run?

Computers run using binary. Computers are actually millions of little switches that swap between on and off to represent data, and are changed using logic. On and off is two states, does that sound familiar? That’s right, this is binary. One of the key parts of computers is logic gates. When a logic gate outputs true or false a computer might flip one of it’s switches to display a change on the screen or new data stored. We will go over each logic gate here.

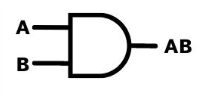
And Gate

The first and one of the simplest gates is the and gate, this gate takes two inputs and compares them to eachother, if both inputs are true then the gate outputs true

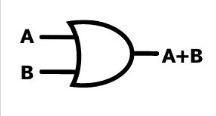
Or Gate

The second gate we cover is the or gate, this gate checks the inputs and if either one is true then the output is true. This includes when both inputs are true

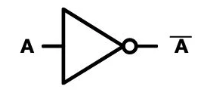
Not Gate

While not really being a gate, this is akin to a function and takes only one input, and flips it. So a true statement would become false and a false would become true.

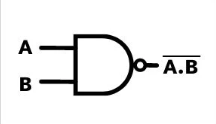
Nand Gate

This gate is a combination of the not gate and the and gate, the idea is that it flips outputs of a and gate. Otherwise it functions the exact same.

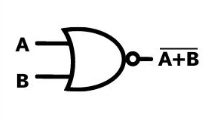
Nor Gate

Similar to the nand gate, this gate is the combination of a or and a not gate. It takes the same inputs of a or gate and outputs the sameway, but then takes the output and puts it through a not gate

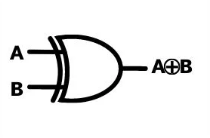
Xor Gate

This gate is unique, but can be incredibly useful. A xor gate is a combination of the nand gate and the or gate. It takes two inputs, and when one or the other is true, it will output true. However different to the or gate, when both inputs are true a xor gate will output false similar to the nand gate.

These gates make up the logic that a computer uses in order to determine what switches to flip and is the idea behind all the logic a computer handles in its hardware, even in the CPU, RAM, and Motherboard